2016/02/14(日) [n年前の日記]
#1 [prog][dxruby] スプライン曲線について調べてたり
3次スプライン曲線、とやらが気になってきたのです。Catmull-Romスプラインと比べて結果は違うのかな、どうなのかな、と。
◎ 3次スプライン曲線を Ruby + DXRubyで試したり。 :
以下、参考ページ。
_[PHP]3次スプライン曲線を使ったスプライン補間 | PHP Archive
_数値計算
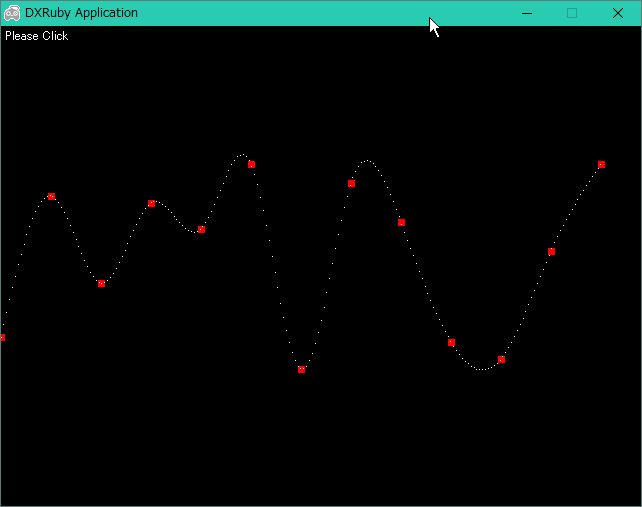
Ruby + DXRuby に移植して動作確認してみたり。
スクリプトを起動後、ウインドウ内でマウスクリックすると、各点の配置が全部変わりますよ、とメモ。
_cubic_spline.rb
ベタ移植してるうちに気がついたのだけど。コレってもしかして、x が必ずプラス方向に増えていくことが前提の実装…なのでは…。グラフを描く時はたしかにそのほうが都合がいいわけだけど、自分の場合、ゲームっぽい何かに使えないかと思いながら実験してるので、各点を自由に配置できないとなると、ちょっと使いどころが…。
_[PHP]3次スプライン曲線を使ったスプライン補間 | PHP Archive
_数値計算
Ruby + DXRuby に移植して動作確認してみたり。
スクリプトを起動後、ウインドウ内でマウスクリックすると、各点の配置が全部変わりますよ、とメモ。
_cubic_spline.rb
# DXRubyで3次スプライン曲線を描画
# xが右方向に増えていくことが前提、らしい?
#
# 参考ページ
#
# [PHP]3次スプライン曲線を使ったスプライン補間 | PHP Archive
# http://php-archive.net/php/cubic-spline/
#
# 数値計算
# http://www.sist.ac.jp/~suganuma/kougi/other_lecture/SE/num/num.htm#7.2
require 'dxruby'
# 3次スプライン補間
class CubicSpline
# コンストラクタ
# @param [Array] poslist [x,y]の配列群
def initialize(poslist)
init(poslist)
end
# 係数を計算して記憶
# @param [Array] poslist [x,y]の配列群
def init(poslist)
@n = poslist.length - 1
@h = []
@b = []
@d = []
@g = []
@u = []
@q = []
@s = []
@r = []
@x = []
@y = []
poslist.each do |px, py|
@x.push(px.to_f)
@y.push(py.to_f)
end
# step 1
0.step(@n - 1, 1) do |i|
@h[i] = @x[i + 1] - @x[i]
end
1.step(@n - 1, 1) do |i|
@b[i] = 2.0 * (@h[i] + @h[i - 1])
@d[i] = 3.0 * ((@y[i+1] - @y[i]) / @h[i] - (@y[i] - @y[i-1]) / @h[i-1])
end
# step 2
@g[1] = @h[1] / @b[1]
2.step(@n - 2, 1) do |i|
@g[i] = @h[i] / (@b[i] - @h[i-1] * @g[i-1])
end
@u[1] = @d[1] / @b[1]
2.step(@n - 1, 1) do |i|
@u[i] = (@d[i] - @h[i-1] * @u[i-1]) / (@b[i] - @h[i-1] * @g[i-1])
end
# step 3
@r[0] = 0.0
@r[@n] = 0.0
@r[@n-1] = @u[@n-1]
(@n - 2).step(1, -1) do |i|
@r[i] = @u[i] - @g[i] * @r[i+1]
end
# step 4
0.step(@n - 1, 1) do |i|
@q[i] = (@y[i+1] - @y[i]) / @h[i] - @h[i] * (@r[i+1] + 2.0 * @r[i]) / 3.0
@s[i] = (@r[i+1] - @r[i]) / (3.0 * @h[i])
end
end
# 補間値の計算
# @param [Number] x1 補間値を求める値
# @return [Number] 補間値
def get_value(x1)
i = -1.0
i1 = 1
while i1 < @n and i < 0.0
i = i1 - 1 if x1 < @x[i1]
i1 += 1
end
i = @n - 1 if i < 0.0
xx = x1 - @x[i]
y1 = @y[i] + xx * (@q[i] + xx * (@r[i] + @s[i] * xx))
return y1
end
end
if $0 == __FILE__
# ----------------------------------------
# 動作テスト
# 四角を描画
# @param [Number] x x座標
# @param [Number] y y座標
# @param [Number] sz サイズ
# @param [Array] col 色。[r, g, b]の配列
def draw_dot(x, y, sz, col)
sz /= 2.0
Window.drawBoxFill(x - sz, y - sz, x + sz, y + sz, col)
end
# 点を描画
# @param [Number] x x座標
# @param [Number] y y座標
# @param [Array] col 色。[r, g, b]の配列
def draw_dot2(x, y, color)
Window.drawLine(x, y, x, y, color)
end
# 座標群を乱数で生成
# @return [Array] [x0,y0],[x1,y1]...[xn,yn]の配列を生成して返す
def get_poslist
poslist = []
w = Window.width
h = Window.height
0.step(w, 50) do |x|
y = rand(h / 2) + (h / 4)
poslist.push([x, y])
end
return poslist
end
fnt = Font.new(12)
poslist = get_poslist
spline = CubicSpline.new(poslist)
# メインループ
Window.loop do
break if Input.keyPush?(K_ESCAPE) # ESCキーで終了
if Input.mousePush?(M_LBUTTON)
# マウスボタンが押されたら座標群を生成し直し
poslist = get_poslist
spline.init(poslist)
end
# 制御点を描画
poslist.each do |x, y|
draw_dot(x, y, 6, C_RED)
end
# 3次スプラインを描画
end_x1 = poslist.last[0]
x1 = 0.0
x1_add = end_x1.to_f / (poslist.length * 16)
while x1 <= (end_x1 + 0.01)
y1 = spline.get_value(x1)
draw_dot2(x1, y1, C_WHITE)
x1 += x1_add
end
Window.drawFont(4, 4, "Please Click", fnt)
end
end
ベタ移植してるうちに気がついたのだけど。コレってもしかして、x が必ずプラス方向に増えていくことが前提の実装…なのでは…。グラフを描く時はたしかにそのほうが都合がいいわけだけど、自分の場合、ゲームっぽい何かに使えないかと思いながら実験してるので、各点を自由に配置できないとなると、ちょっと使いどころが…。
◎ 別のスプライン曲線を試したり。 :
その後、別の実装をしてる例を見かけたり。
_Flashゲーム講座&ASサンプル集【曲線について】
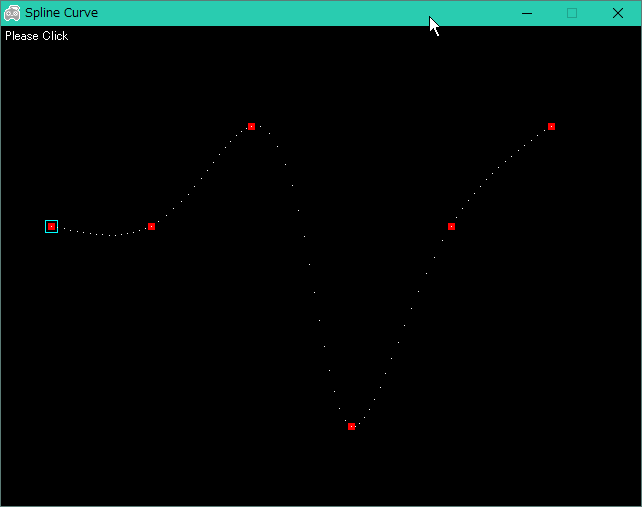
ただ、これは、どんな種類のスプライン曲線なのか記述が無いので、何スプライン曲線なのか分らんのですけれど。とりあえずコレも、Ruby + DXRuby にベタ移植して動作確認してみたり。
スクリプト起動後、ウインドウ内でマウスクリックすると、点の位置を順々に指定できますよ、とメモ。
_spline.rb
これは3次スプライン曲線なのだろうか…。なんだか違う気がする…。Catmull-Rom と形が似てる気もするし…。
_Flashゲーム講座&ASサンプル集【曲線について】
ただ、これは、どんな種類のスプライン曲線なのか記述が無いので、何スプライン曲線なのか分らんのですけれど。とりあえずコレも、Ruby + DXRuby にベタ移植して動作確認してみたり。
スクリプト起動後、ウインドウ内でマウスクリックすると、点の位置を順々に指定できますよ、とメモ。
_spline.rb
# DXRubyでスプライン曲線を描画
# 2次スプラインなのか、3次スプラインかなのか不明
#
# 参考ページ
#
# Flashゲーム講座&ASサンプル集【曲線について】
# http://hakuhin.jp/as/curve.html#CURVE_04
require 'dxruby'
require 'pp'
# スプライン補間用クラス
#
# @attr [Array] result スプライン補間した座標群が配列の形で入る
#
class SplineStream
# x,y座標保持用クラス
class Vec
attr_accessor :x
attr_accessor :y
def initialize(x, y)
@x = x.to_f
@y = y.to_f
end
end
attr_accessor :result
# コンストラクタ
# @param [Array] poslist 座標群。一要素が[x,y]になってる配列
# @param [Number] interpolate 分解度
def initialize(poslist, interpolate)
init(poslist, interpolate)
end
# 座標群から補間値を生成する
# @param [Array] poslist 座標群。一要素が[x,y]になってる配列
# @param [Number] interpolate 分解度
def init(poslist, interpolate)
@num = poslist.length
@l = []
@aa = []
@bb = []
@cc = []
p = []
poslist.each do |d|
p.push(Vec.new(d[0], d[1]))
end
0.step(@num - 2, 1) do |i|
p0 = p[i]
p1 = p[i+1]
@l[i] = Math.sqrt((p0.x - p1.x) * (p0.x - p1.x) + (p0.y - p1.y) * (p0.y - p1.y))
end
@aa[0] = [0.0, 1.0, 0.5]
@bb[0] = {
:x => (3.0 / (2.0 * @l[0])) * (p[1].x - p[0].x),
:y => (3.0 / (2.0 * @l[0])) * (p[1].y - p[0].y)
}
@aa[@num - 1] = [1.0, 2.0, 0.0]
@bb[@num - 1] = {
:x => (3.0 / @l[@num - 2]) * (p[@num - 1].x - p[@num - 2].x),
:y => (3.0 / @l[@num - 2]) * (p[@num - 1].y - p[@num - 2].y)
}
1.step(@num - 2, 1) do |i|
a = @l[i - 1]
b = @l[i]
@aa[i] = [b, 2.0 * (b + a), a]
@bb[i] = {
:x => (3.0 * (a * a * (p[i + 1].x - p[i].x)) + 3.0 * b * b * (p[i].x - p[i - 1].x)) / (b * a),
:y => (3.0 * (a * a * (p[i + 1].y - p[i].y)) + 3.0 * b * b * (p[i].y - p[i - 1].y)) / (b * a)
}
end
1.step(@num - 1, 1) do |i|
d = @aa[i-1][1] / @aa[i][0]
@aa[i] = [0, @aa[i][1] * d - @aa[i-1][2], @aa[i][2] * d]
@bb[i][:x] = @bb[i][:x] * d - @bb[i - 1][:x]
@bb[i][:y] = @bb[i][:y] * d - @bb[i - 1][:y]
@aa[i][2] /= @aa[i][1]
@bb[i][:x] /= @aa[i][1]
@bb[i][:y] /= @aa[i][1]
@aa[i][1] = 1
end
@cc[@num - 1] = {
:x => @bb[@num-1][:x],
:y => @bb[@num-1][:y]
}
(@num - 1).step(1, -1) do |j|
@cc[j - 1] = {
:x => @bb[j - 1][:x] - @aa[j - 1][2] * @cc[j][:x],
:y => @bb[j - 1][:y] - @aa[j - 1][2] * @cc[j][:y]
}
end
outdata = []
count = 0
0.step(@num - 2, 1) do |i|
a = @l[i]
v00 = p[i].x
v01 = @cc[i][:x]
v02 = (p[i + 1].x - p[i].x) * 3.0 / (a * a) - (@cc[i + 1][:x] + 2 * @cc[i][:x]) / a
v03 = (p[i + 1].x - p[i].x) * (-2.0 / (a * a * a)) + (@cc[i + 1][:x] + @cc[i][:x]) * (1.0 / (a * a))
v10 = p[i].y
v11 = @cc[i][:y]
v12 = (p[i + 1].y - p[i].y) * 3.0 / (a * a) - (@cc[i + 1][:y] + 2 * @cc[i][:y]) / a
v13 = (p[i + 1].y - p[i].y) * (-2.0 / (a * a * a)) + (@cc[i + 1][:y] + @cc[i][:y]) * (1.0 / (a * a))
t = 0.0
t_spd = a.to_f / interpolate.to_f
0.step(interpolate - 1, 1) do |j|
tx = ((v03 * t + v02) * t + v01) * t + v00
ty = ((v13 * t + v12) * t + v11) * t + v10
outdata.push([tx, ty])
t += t_spd
end
end
outdata.push([p[@num-1].x, p[@num-1].y])
@result = outdata
end
end
if $0 == __FILE__
# ----------------------------------------
# 動作確認
Window.caption = "Spline Curve"
# 四角(塗り潰し)を描画
def draw_dot(x, y, sz, col)
sz = sz / 2.0
Window.drawBoxFill(x - sz, y - sz, x + sz, y + sz, col)
end
# 点を描画
def draw_dot2(x, y, col)
Window.drawLine(x, y, x, y, col)
end
# 四角(線のみ)を描画
def draw_box(x, y, sz, col)
sz = sz / 2.0
x1, y1 = x - sz, y - sz
x2, y2 = x + sz, y + sz
Window.drawLine(x1, y1, x2, y1, col)
Window.drawLine(x1, y2, x2, y2, col)
Window.drawLine(x1, y1, x1, y2, col)
Window.drawLine(x2, y1, x2, y2, col)
end
fnt = Font.new(12)
# 1区間を何分割するか
interpolate = 16
# 初期座標群
poslist = [
[50, 200],
[150, 200],
[250, 100],
[350, 400],
[450, 200],
[550, 100],
]
spline = SplineStream.new(poslist, interpolate)
mode = 0
Window.loop do
break if Input.keyPush?(K_ESCAPE)
if Input.mousePush?(M_LBUTTON)
# マウスボタンがクリックされたら座標変更
poslist[mode] = [Input.mousePosX.to_f, Input.mousePosY.to_f]
mode += 1
mode = 0 if mode >= poslist.length
# スプライン曲線を作り直し
spline.init(poslist, interpolate)
end
# 制御点を描画
poslist.each_with_index do |d, i|
x, y = d
draw_dot(x, y, 6, C_RED)
draw_box(x, y, 12, C_CYAN) if i == mode
end
# スプライン曲線を描画
spline.result.each do |d|
x, y = d
draw_dot2(x, y, C_WHITE)
end
Window.drawFont(4, 4, "Please Click", fnt)
end
end
これは3次スプライン曲線なのだろうか…。なんだか違う気がする…。Catmull-Rom と形が似てる気もするし…。
◎ スプライン曲線では道路の自動生成は難しいかも。 :
道路の自動生成に使えないかと、それぞれの曲線描画を試しているのだけど。もしかすると、どれを使っても上手くいかないのではないか、という気がしてきたり。
おそらく、道路の自動生成は、自機の位置がある程度進んだら、新しい制御点を追加、かつ、一番古い手前の制御点を削除して、曲線を再作成、という感じの処理になるのかなと想像しているけど。今まで試したアレコレは、制御点が増えたり減ったりすると、曲線の形が変わってしまうように見えるわけで。つまり、道路用の制御点が増えたり減ったりするたびに、画面の中に見えている道路の形がパカッパカッと潔く変わってしまうのではないか、と。
違う方法を考えたほうがいいのかもしれない…。
おそらく、道路の自動生成は、自機の位置がある程度進んだら、新しい制御点を追加、かつ、一番古い手前の制御点を削除して、曲線を再作成、という感じの処理になるのかなと想像しているけど。今まで試したアレコレは、制御点が増えたり減ったりすると、曲線の形が変わってしまうように見えるわけで。つまり、道路用の制御点が増えたり減ったりするたびに、画面の中に見えている道路の形がパカッパカッと潔く変わってしまうのではないか、と。
違う方法を考えたほうがいいのかもしれない…。
[ ツッコむ ]
以上です。