2012/08/02(木) [n年前の日記]
#1 [javascript] 長方形の詰め込み問題についてまだまだ実験中
とりあえず、BLF法(Bottom-Left-Fill)については動いた。
_長方形詰込み問題のテスト用ページ (2013/10/06 リンク先をDropboxから自宅サーバ内ページに変更)
最初、 _こちらの講義資料のページ のサンプルプログラムを、意味も分からず書き写したのだけど。説明用pdfを、自分が分かるように写経(?)したら、何をやってるか理解できた。写経したpdfは以下。
_BL安定点候補についての説明pdf
_BL法チェックについての説明pdf
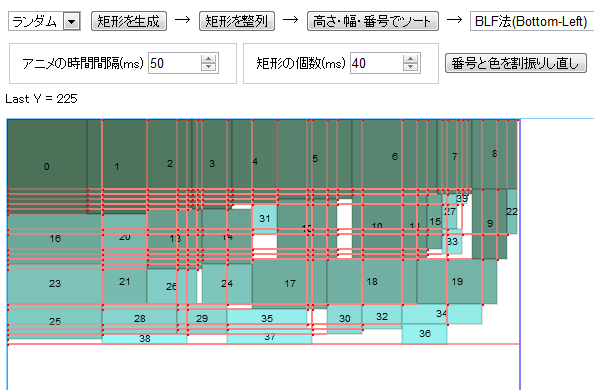
ただ、問題があることも分かったわけで。以下が結果画像だけど。
赤い点が、BL安定点候補の座標。 *1
明らかに、「そこにはもう矩形が置けないだろう… (´・ω・`)」という場所に、BL安定点候補が作られてる。
そして、この全ての候補群に対し、矩形が置けるか、置いたとして他の矩形と重なってないか、てなことを判断していくわけだから…。矩形の数が少ない場合は、他の方法と比べてそんなに処理時間は違わないのだけど。配置済みの矩形が増えるにつれて、どう見てもモリモリと遅くなっていくはずで。
どうせ扱う矩形数は少ないのだからこれでいいじゃん、という気もするのだけど。しかし、もうちょっとどうにかならんか、BL安定点候補を減らせないか、という気もしてきたり。
さて、どうすればいいんだろう?
ちょっと思いつくのは…。
_長方形詰込み問題のテスト用ページ (2013/10/06 リンク先をDropboxから自宅サーバ内ページに変更)
最初、 _こちらの講義資料のページ のサンプルプログラムを、意味も分からず書き写したのだけど。説明用pdfを、自分が分かるように写経(?)したら、何をやってるか理解できた。写経したpdfは以下。
_BL安定点候補についての説明pdf
_BL法チェックについての説明pdf
ただ、問題があることも分かったわけで。以下が結果画像だけど。
赤い点が、BL安定点候補の座標。 *1
明らかに、「そこにはもう矩形が置けないだろう… (´・ω・`)」という場所に、BL安定点候補が作られてる。
そして、この全ての候補群に対し、矩形が置けるか、置いたとして他の矩形と重なってないか、てなことを判断していくわけだから…。矩形の数が少ない場合は、他の方法と比べてそんなに処理時間は違わないのだけど。配置済みの矩形が増えるにつれて、どう見てもモリモリと遅くなっていくはずで。
どうせ扱う矩形数は少ないのだからこれでいいじゃん、という気もするのだけど。しかし、もうちょっとどうにかならんか、BL安定点候補を減らせないか、という気もしてきたり。
さて、どうすればいいんだろう?
ちょっと思いつくのは…。
- メモリが贅沢な環境なら、配置先と同じ大きさの、「矩形が既に描かれてるか否か」だけを判定する画像領域を作って、そこにも矩形を書き込んでいく。BL安定点候補が見つかった際に、その座標には既に矩形が描かれてるなら、BL安定点候補から外す。
- 新しく置いた矩形から線分を伸ばして、配置済み矩形の線分、もしくは配置済み矩形から伸びた仮想の線分との交差座標を記録。新しく置いた矩形から近い順に交差座標を見ていって、仮想線分との交差座標はそのままにして、実際の線分と交差したらそれ以後のBL安定点候補は、候補から外す。
◎ とんでもない勘違いをしてた。 :
BLF法で矩形数を増やして実行すると、矩形数が増えるにつれて遅くなるなあ、と思っていたのだけど。ふと、BL安定点候補の描画を無効にしてみたら、サクサクと処理が進むように。内部計算が遅いのではなくて、canvasの描画処理が遅かったのか…! トホホ。
それはそれとして。矩形を一つ置いて、BL安定点候補群を得るたびに、それら候補群の1つ1つが、配置済み矩形の中に入っているか調べて、入っているなら除去するようにしてみたり。…画面に表示される候補群がグンと少なくなった。
それはそれとして。矩形を一つ置いて、BL安定点候補群を得るたびに、それら候補群の1つ1つが、配置済み矩形の中に入っているか調べて、入っているなら除去するようにしてみたり。…画面に表示される候補群がグンと少なくなった。
◎ JavaScriptの乱数は初期化ができないのか。 :
Math.random() に種を与えて初期化できないのかな、初期化できれば毎回同じランダムな矩形群が得られて実験しやすいのだけど。と思ったけれど、JavaScript の乱数って種を与えることはできないようで。
ということで、 _Mersenne Twister in JavaScript (mt.js) を使わせてもらったり。おそらくこれなら、種を与えることで、乱数の再現性が得られるだろうと。
乱数というか、疑似乱数だけど。
ということで、 _Mersenne Twister in JavaScript (mt.js) を使わせてもらったり。おそらくこれなら、種を与えることで、乱数の再現性が得られるだろうと。
乱数というか、疑似乱数だけど。
*1: 赤い線は、BL安定点候補が、どの矩形と判定し合ってそういう結果を出したのかを示す線。…BL安定点ってのは、Bottom(下)にもLeft(左)にも、それ以上矩形を配置しようがないだろう、と思われる点のこと。自分の作ったページは上下が逆なので、上にも左もそれ以上を矩形を配置できないと思われる点が、BL安定点の候補、になる。そして、このBL安定点候補の一つ一つに対して、まだ配置してない新しい矩形を置けるかな? 置けないかな? と判別処理をしていくことで、詰め込みができるわけで。
[ ツッコむ ]
以上です。