2017/04/06(木) [n年前の日記]
#4 [ruby] 正規乱数とやらが作れそうかテスト
_乱数にコクを出すアレ
が気になり始めたので Ruby + DXRuby を使ってテスト。
_「ちゃんとした正規乱数が欲しいなら Box-Muller を使うべき」 _「sin,cosとか平方根とか今時はたいして重くないし」 という主張も見かけたので、以下を参考にして Box-Muller もテスト。
_Box-Muller法による正規分布列生成 - Qiita
こんな感じのソースでどうだろう。合ってるのだろうか。
_boxmuller.rb
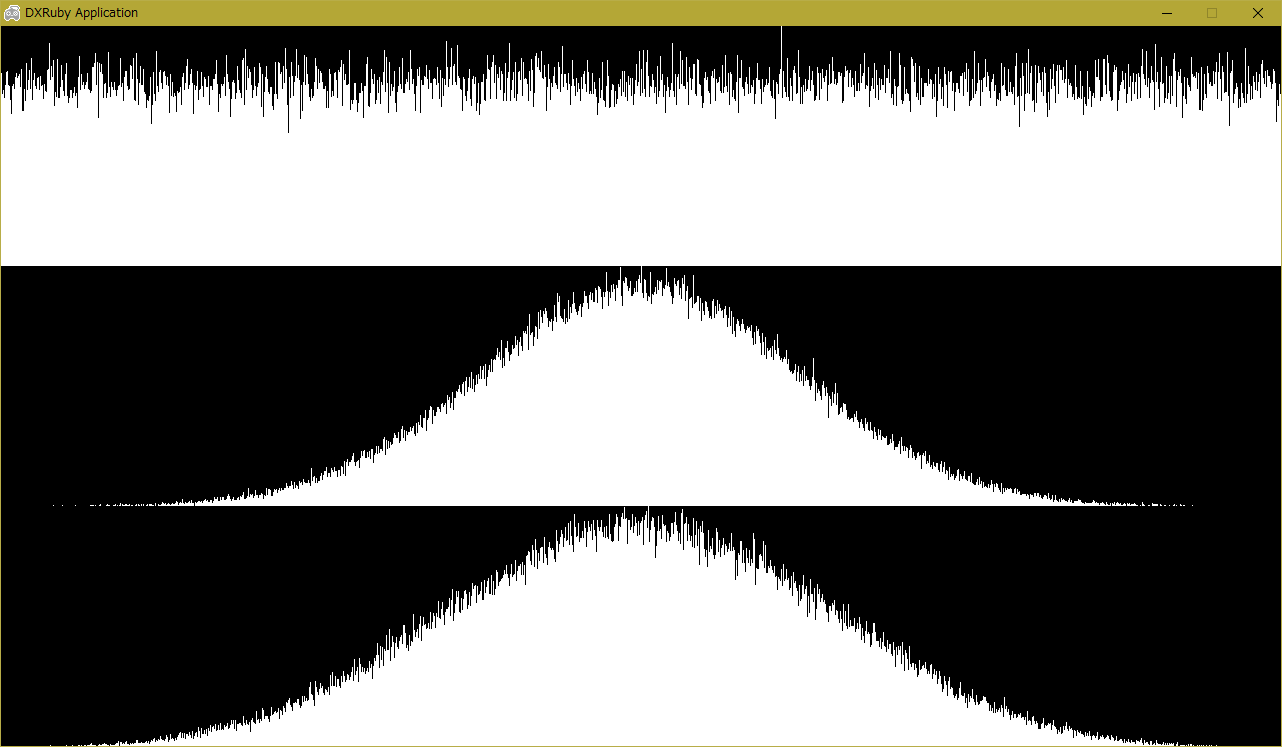
結果はこんな感じに。
上から、只の rand (= 一様分布)、Box-Muller法、乱数にコクを出すアレ。
ゲーム等で使う分には乱数にコクを出すソレでもそこそこ十分っぽい雰囲気。Box-Mullerはどこからどこまでの範囲を取るのかもちと分からんかったし…。
その後、 _「一様乱数の平均値を正規乱数として代用する」という話をゆるふわ統計的に検証する - k11i.biz で、 _Ziggurat法 なるものもあると知った。コレも試せば良かったかしらん。
_「ちゃんとした正規乱数が欲しいなら Box-Muller を使うべき」 _「sin,cosとか平方根とか今時はたいして重くないし」 という主張も見かけたので、以下を参考にして Box-Muller もテスト。
_Box-Muller法による正規分布列生成 - Qiita
こんな感じのソースでどうだろう。合ってるのだろうか。
_boxmuller.rb
# Box-Muller法による正規乱数が作れそうかどうかをテスト
require 'dxruby'
# 乱数の結果を DXRuby の Image に描き込む
def get_image(w, h, data)
# 最大カウント数を取得
m = data.max
# Imageに描き込み
img = Image.new(w, h)
w.times do |x|
cnt = (data[x] * h.to_f / m).to_i
y = h - 1
cnt.times do
img[x, y] = C_WHITE
y -= 1
end
end
return img
end
# Box-Muller法で乱数を取得
def get_box_mular(mu, sigma)
x = rand
y = rand
r = Math.sqrt(-2.0 * Math.log(x)) * Math.cos(2.0 * Math::PI * y)
return r * sigma + mu
end
w, h = 1280, 720
hh = h / 3
tc = 200000
# 一様分布になってるか確認
n = Array.new(w, 0)
tc.times do
r = (rand * w).to_i
n[r] += 1
end
nml_img = get_image(w, hh, n)
# Box-Muller法
n = Array.new(w, 0)
tc.times do
rbm = get_box_mular(0.0, 1.0)
r = (rbm * (w / 8) + (w / 2)).to_i
n[r] += 1 if r >= 0 and r < w
end
bmr_img = get_image(w, hh, n)
# 乱数にコクを出すアレ
n = Array.new(w, 0)
tc.times do
r = 0
cnt = 4
cnt.times { r += rand }
r = ((r / cnt) * w).to_i
n[r] += 1
end
kok_img = get_image(w, hh, n)
# 結果表示
Window.resize(w, h)
Window.loop do
break if Input.keyPush?(K_ESCAPE)
Window.draw(0, 0, nml_img)
Window.draw(0, hh, bmr_img)
Window.draw(0, hh + hh, kok_img)
end
結果はこんな感じに。
上から、只の rand (= 一様分布)、Box-Muller法、乱数にコクを出すアレ。
ゲーム等で使う分には乱数にコクを出すソレでもそこそこ十分っぽい雰囲気。Box-Mullerはどこからどこまでの範囲を取るのかもちと分からんかったし…。
その後、 _「一様乱数の平均値を正規乱数として代用する」という話をゆるふわ統計的に検証する - k11i.biz で、 _Ziggurat法 なるものもあると知った。コレも試せば良かったかしらん。
[ ツッコむ ]
以上です。